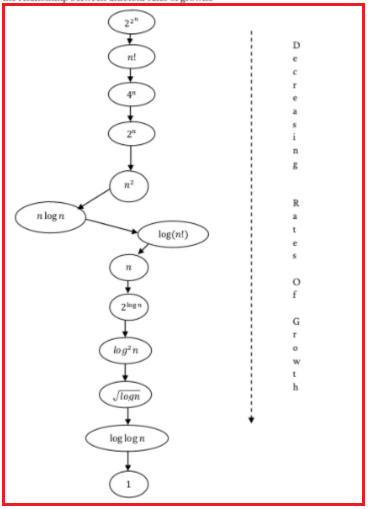
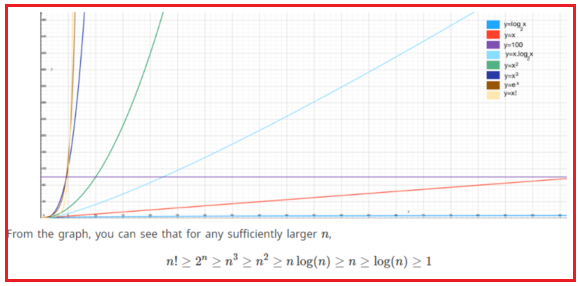
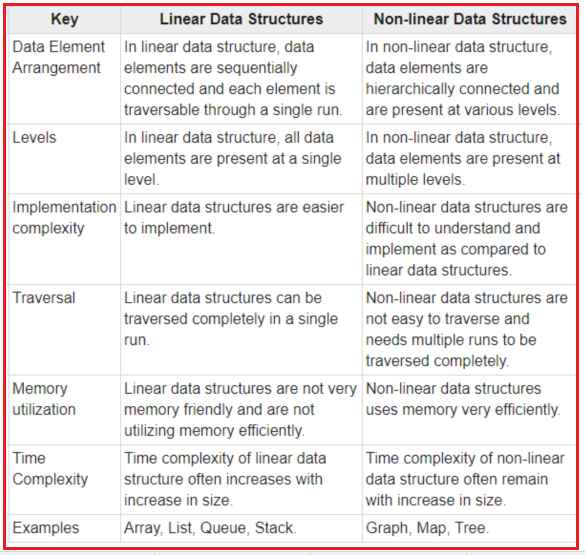
In this article, I am going to discuss Recursion And BackTracking in detail. Please read our previous article where we discussed Master Theorem. In this article, we will look at one of the important topics, “recursion”, which will be used in almost every chapter, and also its relative “backtracking”.
What is Recursion?
Any function which calls itself is called recursive. A recursive method solves a problem by calling a copy of itself to work on a smaller problem. This is called the recursion step. The recursion step can result in many more such recursive calls.
It is important to ensure that the recursion terminates. Each time the function calls itself with a slightly simpler version of the original problem. The sequence of smaller problems must eventually converge on the base case.
Why Recursion?
Recursion is a useful technique borrowed from mathematics. Recursive code is generally shorter and easier to write than iterative code. Generally, loops are turned into recursive functions when they are compiled or interpreted.
Recursion is most useful for tasks that can be defined in terms of similar sub-tasks. For example, sort, search, and traversal problems often have simple recursive solutions.
Format of a Recursive Function
A recursive function performs a task in part by calling itself to perform the subtasks. At some point, the function encounters a subtask that it can perform without calling itself. This case, where the function does not recur, is called the base case. The former, where the function calls itself to perform a subtask, is referred to as the recursive case. We can write all recursive functions using the format:
As an example consider the factorial function: n! is the product of all integers between n and 1.The definition of recursive factorial looks like:
This definition can easily be converted to recursive implementation. Here the problem is determining the value of n!, and the subproblem is determining the value of (n – l)!. In the recursive case, when n is greater than 1, the function calls itself to determine the value of (n – l)! and multiplies that with n.
In the base case, when n is 0 or 1, the function simply returns 1. This looks like the following:
Recursion and Memory (Visualization)
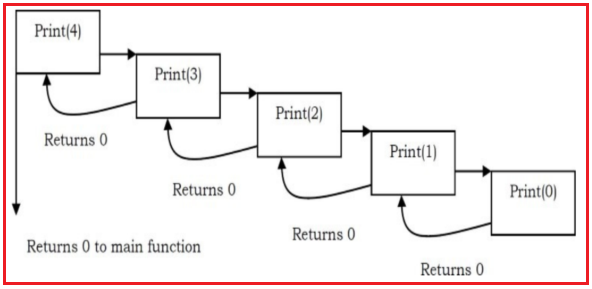
Each recursive call makes a new copy of that method (actually only the variables) in memory. Once a method ends (that is, returns some data), the copy of that returning method is removed from memory. The recursive solutions look simple but visualization and tracing take time. For better understanding, let us consider the following example.
For this example, if we call the print function with n=4, visually our memory assignments may look like:
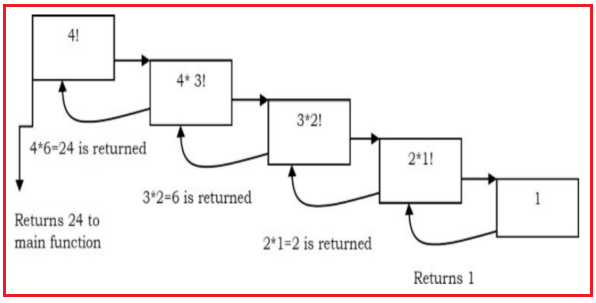
Now, let us consider our factorial function. The visualization of factorial function with n=4 will look like:
Recursion versus Iteration
While discussing recursion, the basic question that comes to mind is: which way is better? –iteration or recursion? The answer to this question depends on what we are trying to do. A recursive approach mirrors the problem that we are trying to solve. A recursive approach makes it simpler to solve a problem that may not have the most obvious of answers. But, recursion adds overhead for each recursive call (needs space on the stack frame).
Recursion
In this chapter, we cover a few problems with recursion and we will discuss the rest in other chapters. By the time you complete reading the entire book, you will encounter many recursion problems.
Problem-1 Discuss Towers of Hanoi puzzle.
Solution: The Towers of Hanoi is a mathematical puzzle. It consists of three rods (or pegs or towers), and a number of disks of different sizes which can slide onto any rod. The puzzle starts with the disks on one rod in ascending order of size, the smallest at the top, thus making a conical shape. The objective of the puzzle is to move the entire stack to another rod, satisfying the following rules:
Algorithm:
Problem-2: Given an array, check whether the array is in sorted order with recursion.
Solution:
Time Complexity: O(n). Space Complexity: O(n) for recursive stack space.
What is Backtracking?
Backtracking is an improvement of the brute force approach. It systematically searches for a solution to a problem among all available options. In backtracking, we start with one possible option out of many available options and try to solve the problem if we are able to solve the problem with the selected move then we will print the solution else we will backtrack and select some other option and try to solve it. If none of the options work out we will claim that there is no solution for the problem.
Backtracking is a form of recursion. The usual scenario is that you are faced with a number of options, and you must choose one of these. After you make your choice you will get a new set of options; just what set of options you get depends on what choice you made. This procedure is repeated over and over until you reach a final state. If you made a good sequence of choices, your final state is a goal state; if you didn’t, it isn’t.
Backtracking can be thought of as a selective tree/graph traversal method. The tree is a way of representing some initial starting position (the root node) and a final goal state (one of the leaves). Backtracking allows us to deal with situations in which a raw brute-force approach would explode into an impossible number of options to consider. Backtracking is a sort of refined brute force. At each node, we eliminate choices that are obviously not possible and proceed to recursively check only those that have potential.
What’s interesting about backtracking is that we back up only as far as needed to reach a previous decision point with an as-yet-unexplored alternative. In general, that will be at the most recent decision point. Eventually, more and more of these decision points will have been fully explored, and we will have to backtrack further and further. If we backtrack all the way to our initial state and have explored all alternatives from there, we can conclude the particular problem is unsolvable. In such a case, we will have done all the work of the exhaustive recursion and known that there is no viable solution possible.
Backtracking speeds the exhaustive search by pruning.
Example Algorithms of Backtracking
Problem-3 Generate all the strings of n bits. Assume A[0..n – 1] is an array of size n.
Solution:
Let T(n) be the running time of binary(n). Assume function printf takes time O(1).
Using Subtraction and Conquer Master theorem we get T(n) = O(2n). This means the algorithm for generating bit-strings is optimal.
Problem-4 Generate all the strings of length n drawn from 0… k – 1.
Solution: Let us assume we keep the current k-ary string in an array A[0.. n – 1]. Call function kstring(n, k):
Let T(n) be the running time of k – string(n). Then,
Using Subtraction and Conquer Master theorem we get T(n) = O(kn).
Note: For more problems, refer to the String Algorithms chapter.
Problem-5 Finding the length of connected cells of 1s (regions) in a matrix of Os and 1s: Given a matrix, each of which maybe 1 or 0. The filled cells are connected form a region. Two cells are said to be connected if they are adjacent to each other horizontally, vertically, or diagonally. There may be several regions in the matrix. How do you find the largest region (in terms of the number of cells) in the matrix?
Solution: The simplest idea is: for each location traverse in all 8 directions and in each of those directions keep track of maximum region found.
Problem-6 Solve the recurrence T(n) = 2T(n – 1) + 2n.
Solution: At each level of the recurrence tree, the number of problems is double from the previous level, while the amount of work being done in each problem is half from the previous level. Formally, the ith level has 2i problems, each requiring 2n–i work. Thus the ith level requires exactly 2n work. The depth of this tree is n, because at the ith level, the originating call will be T(n – i). Thus the total complexity for T(n) is T(n2n).
Here, in this article, I try to explain Recursion And BackTracking. I hope you enjoy this Recursion And BackTracking article. I would like to have your feedback. Please post your feedback, question, or comments about this article.
Summary:
I hope this post will be helpful to understand the concept of Recursion And Back Tracking
Please share this post with your friends and colleagues.
For any queries please post a comment below.
Happy Coding 😉
What is Recursion?
Any function which calls itself is called recursive. A recursive method solves a problem by calling a copy of itself to work on a smaller problem. This is called the recursion step. The recursion step can result in many more such recursive calls.
It is important to ensure that the recursion terminates. Each time the function calls itself with a slightly simpler version of the original problem. The sequence of smaller problems must eventually converge on the base case.
Why Recursion?
Recursion is a useful technique borrowed from mathematics. Recursive code is generally shorter and easier to write than iterative code. Generally, loops are turned into recursive functions when they are compiled or interpreted.
Recursion is most useful for tasks that can be defined in terms of similar sub-tasks. For example, sort, search, and traversal problems often have simple recursive solutions.
Format of a Recursive Function
A recursive function performs a task in part by calling itself to perform the subtasks. At some point, the function encounters a subtask that it can perform without calling itself. This case, where the function does not recur, is called the base case. The former, where the function calls itself to perform a subtask, is referred to as the recursive case. We can write all recursive functions using the format:
As an example consider the factorial function: n! is the product of all integers between n and 1.The definition of recursive factorial looks like:
This definition can easily be converted to recursive implementation. Here the problem is determining the value of n!, and the subproblem is determining the value of (n – l)!. In the recursive case, when n is greater than 1, the function calls itself to determine the value of (n – l)! and multiplies that with n.
In the base case, when n is 0 or 1, the function simply returns 1. This looks like the following:
Recursion and Memory (Visualization)
Each recursive call makes a new copy of that method (actually only the variables) in memory. Once a method ends (that is, returns some data), the copy of that returning method is removed from memory. The recursive solutions look simple but visualization and tracing take time. For better understanding, let us consider the following example.
For this example, if we call the print function with n=4, visually our memory assignments may look like:
Now, let us consider our factorial function. The visualization of factorial function with n=4 will look like:
Recursion versus Iteration
While discussing recursion, the basic question that comes to mind is: which way is better? –iteration or recursion? The answer to this question depends on what we are trying to do. A recursive approach mirrors the problem that we are trying to solve. A recursive approach makes it simpler to solve a problem that may not have the most obvious of answers. But, recursion adds overhead for each recursive call (needs space on the stack frame).
Recursion
- Terminates when a base case is reached.
- Each recursive call requires extra space on the stack frame (memory).
- If we get infinite recursion, the program may run out of memory and result in stack overflow.
- Solutions to some problems are easier to formulate recursively.
- Terminates when a condition is proven to be false.
- Each iteration does not require extra space.
- An infinite loop could loop forever since there is no extra memory being created.
- Iterative solutions to a problem may not always be as obvious as a recursive solution.
- Recursive algorithms have two types of cases, recursive cases, and base cases.
- Every recursive function case must terminate at a base case.
- Generally, iterative solutions are more efficient than recursive solutions [due to the overhead of function calls].
- A recursive algorithm can be implemented without recursive function calls using a stack, but it’s usually more trouble than its worth. That means any problem that can be solved recursively can also be solved iteratively.
- For some problems, there are no obvious iterative algorithms.
- Some problems are best suited for recursive solutions while others are not.
- Fibonacci Series, Factorial Finding
- Merge Sort, Quick Sort
- Binary Search
- Tree Traversals and many Tree Problems: InOrder, PreOrder PostOrder
- Graph Traversals: DFS [Depth First Search] and BFS [Breadth First Search]
- Dynamic Programming Examples
- Divide and Conquer Algorithms
- Towers of Hanoi
- Backtracking Algorithms [we will discuss in the next section]
In this chapter, we cover a few problems with recursion and we will discuss the rest in other chapters. By the time you complete reading the entire book, you will encounter many recursion problems.
Problem-1 Discuss Towers of Hanoi puzzle.
Solution: The Towers of Hanoi is a mathematical puzzle. It consists of three rods (or pegs or towers), and a number of disks of different sizes which can slide onto any rod. The puzzle starts with the disks on one rod in ascending order of size, the smallest at the top, thus making a conical shape. The objective of the puzzle is to move the entire stack to another rod, satisfying the following rules:
- Only one disk may be moved at a time.
- Each move consists of taking the upper disk from one of the rods and sliding it onto
Algorithm:
- Move the top n – 1 disk from Source to Auxiliary tower,
- Move the nth disk from Source to Destination tower,
- Move the n – 1 disks from Auxiliary tower to Destination tower.
- Transferring the top n – 1 disks from Source to Auxiliary tower can again be thought of as a fresh problem and can be solved in the same manner. Once we solve Towers of Hanoi with three disks, we can solve it with any number of disks with the above algorithm.
Problem-2: Given an array, check whether the array is in sorted order with recursion.
Solution:
Time Complexity: O(n). Space Complexity: O(n) for recursive stack space.
What is Backtracking?
Backtracking is an improvement of the brute force approach. It systematically searches for a solution to a problem among all available options. In backtracking, we start with one possible option out of many available options and try to solve the problem if we are able to solve the problem with the selected move then we will print the solution else we will backtrack and select some other option and try to solve it. If none of the options work out we will claim that there is no solution for the problem.
Backtracking is a form of recursion. The usual scenario is that you are faced with a number of options, and you must choose one of these. After you make your choice you will get a new set of options; just what set of options you get depends on what choice you made. This procedure is repeated over and over until you reach a final state. If you made a good sequence of choices, your final state is a goal state; if you didn’t, it isn’t.
Backtracking can be thought of as a selective tree/graph traversal method. The tree is a way of representing some initial starting position (the root node) and a final goal state (one of the leaves). Backtracking allows us to deal with situations in which a raw brute-force approach would explode into an impossible number of options to consider. Backtracking is a sort of refined brute force. At each node, we eliminate choices that are obviously not possible and proceed to recursively check only those that have potential.
What’s interesting about backtracking is that we back up only as far as needed to reach a previous decision point with an as-yet-unexplored alternative. In general, that will be at the most recent decision point. Eventually, more and more of these decision points will have been fully explored, and we will have to backtrack further and further. If we backtrack all the way to our initial state and have explored all alternatives from there, we can conclude the particular problem is unsolvable. In such a case, we will have done all the work of the exhaustive recursion and known that there is no viable solution possible.
- Sometimes the best algorithm for a problem is to try all possibilities.
- This is always slow, but there are standard tools that can be used to help.
Backtracking speeds the exhaustive search by pruning.
Example Algorithms of Backtracking
- Binary Strings: generating all binary strings
- Generating k – ary Strings
- N-Queens Problem
- The Knapsack Problem
- Generalized Strings
- Hamiltonian Cycles [refer to Graphs chapter]
- Graph Coloring Problem
Problem-3 Generate all the strings of n bits. Assume A[0..n – 1] is an array of size n.
Solution:
Let T(n) be the running time of binary(n). Assume function printf takes time O(1).
Using Subtraction and Conquer Master theorem we get T(n) = O(2n). This means the algorithm for generating bit-strings is optimal.
Problem-4 Generate all the strings of length n drawn from 0… k – 1.
Solution: Let us assume we keep the current k-ary string in an array A[0.. n – 1]. Call function kstring(n, k):
Let T(n) be the running time of k – string(n). Then,
Using Subtraction and Conquer Master theorem we get T(n) = O(kn).
Note: For more problems, refer to the String Algorithms chapter.
Problem-5 Finding the length of connected cells of 1s (regions) in a matrix of Os and 1s: Given a matrix, each of which maybe 1 or 0. The filled cells are connected form a region. Two cells are said to be connected if they are adjacent to each other horizontally, vertically, or diagonally. There may be several regions in the matrix. How do you find the largest region (in terms of the number of cells) in the matrix?
Solution: The simplest idea is: for each location traverse in all 8 directions and in each of those directions keep track of maximum region found.
Problem-6 Solve the recurrence T(n) = 2T(n – 1) + 2n.
Solution: At each level of the recurrence tree, the number of problems is double from the previous level, while the amount of work being done in each problem is half from the previous level. Formally, the ith level has 2i problems, each requiring 2n–i work. Thus the ith level requires exactly 2n work. The depth of this tree is n, because at the ith level, the originating call will be T(n – i). Thus the total complexity for T(n) is T(n2n).
Here, in this article, I try to explain Recursion And BackTracking. I hope you enjoy this Recursion And BackTracking article. I would like to have your feedback. Please post your feedback, question, or comments about this article.
Summary:
I hope this post will be helpful to understand the concept of Recursion And Back Tracking
Please share this post with your friends and colleagues.
For any queries please post a comment below.
Happy Coding 😉


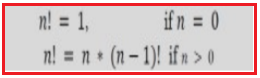







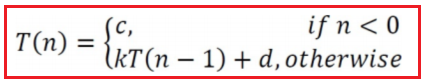
















![Big-O Notation [Upper Bounding Function] Big-O Notation [Upper Bounding Function]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiSY_F_EgdNb1NZqI2VIjq6Z_B-S75Ha160ZKiDQ_pidywRmYdZfZD0ptCmv5uvG4zFKrP0B6mjwOzfzKClDD8Pu97HvIwypGauPRiRv2NU23x_VlzOCjhQeSXzh80G_f95IYF6DjOSIlBZ/s640/word-image-134.png)
![Omega-Q Notation [Lower Bounding Function] Omega-Q Notation [Lower Bounding Function]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgzJYe775iVeW6yHol50Rqicqi-2Xqdkm5F8IIflivKXZIlnNd70nlm9djwmgEyBS_3Rv9LWEHtr580e9gJbC7hyphenhyphen_jH1hQZMkumYLZBpm0f0n0-fssJUx1htG_DONETNsNqdHKFb-bsaTPZ/s640/word-image-135.png)
![Theta-Θ Notation [Order Function] Theta-Θ Notation [Order Function]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh-H5-Jn1KoDvC__bNtU_z-Cq63xfXfe5Bqcsunhi4v9KEmsEdWgIpILoTr3YrzMt8rFGQN0WsMhzqXIYG3g7qtUJ08JVFjOGTuapAC_bFkWdbfdwhSNuTWE31alOPwlNGCNrSV9zJTPdZi/s640/word-image-136.png)